serious stuff
www.cubbi.com
personal
programming
fibonacci numbers
forth examples
postscript examples
muf examples
joy examples
j examples
scheme examples
hope examples
ocaml examples
haskell examples
prolog examples
c++ examples
java examples
assembly language examples
fortran examples
c examples
sh examples
awk examples
perl examples
tcl examples
asmix
hacker test
resume
science
martial arts
fun stuff
www.cubbi.org
|
Fibonacci numbers are defined as follows
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2)
for negative n: F(-n) = (-1)n+1F(n)
Note that examples and benchmarks made before september 2009 on this page use
the older, less general, definition, with F(0) = 1.
September 2009 UPDATE:
UPDATE IN PROGRESS: Five years since I wrote this page, I've decided to rewrite
all examples to be more useful, the subroutines will be as general as
possible (no more 2x2 matrix multiplication), all code will be commented,
each example will now take its arguments from command line (where possible)
April 2014 UPDATE:
This effort was abandoned somewhere in 2010.
ALGORITHMS AND BENCHMARKS SUMMARY
| 1. EXPONENTIAL COMPLEXITY |
|---|
1A - naive binary recursion
execution time: T(n)=to*φn |
asm
java
C |
to=2.8 ns
to=3.0 ns
to=3.1 ns |
| 2. LINEAR COMPLEXITY |
|---|
| 1B - cached binary recursion / memoization |
pending 2009/2010 update |
| 2A - cached linear recursion / infinite lazy-evaluated list |
pending 2009/2010 update |
| 2B - linear recursion with accumulator |
pending 2009/2010 update |
| 2C - imperative loop with mutable variables |
pending 2009/2010 update |
| 3. LOGARITHMIC COMPLEXITY |
|---|
| 3A - matrix multiplication |
pending 2009/2010 update |
| 3B - fast recursion |
pending 2009/2010 update |
| 3C - Binet's formula with rounding |
pending 2009/2010 update |
EXAMPLES
ALGORITHMS AND BENCHMARKS IN DETAIL
Please remember that these benchmarks do not show strength or weakness of any
programming language. All they show is how efficient specific language
translators are at implementing the featured algorithms. It is currently
(as of 2009) in the transitional stage from OLD to NEW benchmarks using modern
hardware and better written examples.
Benchmarked on Intel Pentium Core i7 2.66GHz running Linux 2.6.31 with 12GB RAM, in x86_64 mode
OLD benchmarks: Intel Pentium 4 2.20GHz running Linux 2.5.75 with 640M RAM
NEW RAW BENCHMARK DATA available if you want to see them, as well as
OLD RAW BENCHMARK DATA.
| ALGORITHM 1A: NAIVE BINARY RECURSION |
|---|
- If n equals 0, return 0
- If n equals 1, return 1
- Recursively calculate F(n-1)
- Recursively calculate F(n-2)
- Return the sum of the results from steps 2 and 3
Complexity (fixed precision): O(exp n) speed, O(exp n) space
The number of additions grows exponentially with n, and each recursive call
requires memorization of state (since neither call is tail-recursive), which
makes space complexity also exponential.
This algorithm becomes uselessly slow for F(n) with n>50 and all measured
results easily fit in 64-bit integer data type. With the duration of
the integer arithmetic operations independent of n, the time to execute these
programs is almost perfectly t0φn,
which is why the plots of the logarithm of execution time vs. n are
parallel straight lines.
This algorithm was implemented directly in all languages featured on this web
page, since all of them allow recursion. Only Fortran did not allow recursion
in the past, but it is supported since the 1990 standard.
Curiously, Java outperforms C++ on this test, but it's one of the very few
artifical tests
where it does so
|
| Language | Translator [*] | T0 | T(46),
seconds | |
|---|
| Assembly |
GNU as 2.19.1 [c] |
2.8 ns |
11.63 |
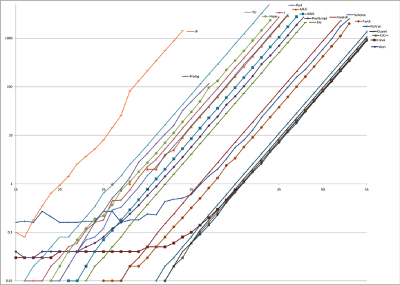
log(Execution time, seconds) vs. Fibonacci number calculated
|
| Java |
Sun Java SE 1.6.0_16-b01 / HotSpot 64-Bit VM 14.2-b01 [b] |
3.0 ns |
12.34 |
| C |
GNU gcc 4.4.1 [c] |
3.1 ns |
12.57 |
| C++ |
GNU g++ 4.4.1 [c] |
3.1 ns |
12.61 |
| OCaml |
INRIA OCaml 3.11.1 [c] |
3.4 ns |
13.98 |
| Fortran |
GNU gfortran 4.4.1 [i] |
4.3 ns |
17.62 |
| Forth |
GNU gforth 0.7.0 [i] |
15.3 ns |
61.91 |
| Scheme |
MIT Scheme 7.7.90 20090107 [b] |
22.6 ns |
98.04 |
| Haskell |
GHC 6.8.2 [c] |
31.3 ns |
129.1 |
| Joy |
Joy1 by Manfred von Thun, 07-May-03 [i] |
199 ns |
813.5 |
| PostScript |
GPL Ghostscript 8.70 [i] |
284 ns |
1147 |
| awk |
GNU Awk 3.1.7 [i] |
417 ns |
1729 |
| MUF |
FuzzBall MUCK 6.09 [b] |
716 ns |
2939 |
| perl |
perl 5.8.8 [i] |
755 ns |
3101 |
| J |
Jsoftware J64 6.02 [i] |
1.08 μs |
4386 |
| Hope |
Hope by Ross Paterson, 08-Dec-03 [i] |
1.52 μs |
6035 |
| Prolog |
SWI Prolog 5.6.64 [b] |
2.17 μs |
8900 |
| Tcl |
Tcl 8.5.7 [i] |
3.37 μs |
13700 |
| sh |
bash 4.0.33(2) [i] |
101 μs |
415000 |
| |
|
|
|
[*] - [c] for Compiler, [b] for Bytecode intepreter, [i] for Interpreter
Execution time is user time as reported by time(1) except for MUF, where an internal time function was called from the program.
T(46) was measured directly only when it was less than 2000 seconds, otherwise it was extrapolated from execution times for smaller inputs.
In all cases I tried to pick the fastest one of the language translators that are readily available and
offer unlimited precision integer arithmetics (it becomes important in further tests).
| ALGORITHM 1B: CACHED BINARY RECURSION / MEMOIZATION |
|---|
- If n equals 0, return 0
- If n equals 1, return 1
- Read F(n-1) from cache or recursively calculate if not cached yet
- Read F(n-2) from cache or recursively calculate if not cached yet
- Return the sum of the results from steps 2 and 3 and save it in the cache
Complexity (unlimited precision): O(n2) speed, O(exp n) space
The common optimization technique applied to binary recursions is memoization:
for any given set of arguments, the recursive function is calculated only once,
and the result is stored in memory. Further calls to the function with the same
arguments return the previously calculated result.
Since no function result is calculated twice, the number of additions
required to calculate F(n) is reduced to n. The number of cache lookups
is instead exponential but, assuming it is implemented as a suitable
random-access data structure (array or hash table), the time of each
cache lookup is O(1).
Space requirements for this algorithm are still exponential because of
binary recursion.
In the programming languages that have built-in support for memoization
(such as J or Factor), algorithm 1A can be turned into 1B with just one
keyword. For other languages, I manually implement a suitably generic data
structure.
|
| Language | Translator [*] | t0 | T(1,000,000),
seconds | |
|---|
| |
|
|
|

sqrt(Execution time, seconds) vs. Fibonacci number calculated
|
| |
|
|
|
[*] - [c] for Compiler, [b] for Bytecode intepreter, [i] for Interpreter
Execution time is user time as reported by time(1), the test programs were
modified to avoid conversion of the entire result to string, since that
operation may be slow for large numbers.
| ALGORITHM 2A: CACHED LINEAR RECURSION |
|---|
When previously calculated Fibonacci numbers are stored in a data structure,
there is no need for binary recursion, the entire structure can be filled
with only n iterations.
- infinite lazy evaluated list.
- Construct an infinite list F with F[0] equal 0 and F[1] equal 1
- Define F[i] as the sum of F[n-1] and F[n-2].
- Return the nth element of the list
In the languages that support lazy evaluation, either implicitly (like Hope
or Haskell) or explicitly (like OCaml or Scheme), it is possible to
construct the data structure containing all Fibonacci numbers and simply
return the nth element of the structure.
- random-access container.
- Create a container F with the elements F[0] equal 0 and F[1] equal 1
- Recursively (or iteratively) calculate the elements F[2..n]
according to the formula F[i]=F[i-1]+F[i-2]
- Return F[n]
In the languages that only support eager evaluation, the entire data
structure must be filled with an explicit loop (or a tail-recursive function).
If the container permits random access with O(1) complexity, the total
execution complexity is O(n), assuming fixed precision. For large precision
numbers, the complexity of addition grows with n as well.
- Complexity (fixed precision): O(n) speed, O(n) space
Complexity (unlimited precision): O(n2) speed, O(n2) space.
|
| Language | Translator [*] | t0 | T(1,000,000),
seconds | |
|---|
| |
|
|
|

sqrt(Execution time, seconds) vs. Fibonacci number calculated
|
| |
|
|
|
[*] - [c] for Compiler, [b] for Bytecode intepreter, [i] for Interpreter
Execution time is user time as reported by time(1), the test programs were
modified to avoid conversion of the entire result to string, since that
operation may be slow for large numbers.
| ALGORITHM 2B: LINEAR RECURSION WITH ACCUMULATOR |
|---|
- Define a recursive function λ(n1,n2,n) such as
- λ(n1,n2,n) returns 0, if n=0 and 1 if n=1
- λ(n1,n2,n) return the result of
λ(n2,n1+n2,n-1), if n>1
- Return the result of λ(0,1,n)
Complexity (fixed precision): O(n) speed, O(1) space
Complexity (unlimited precision): O(n2) speed, O(n) space
These algorithms execute n additions to calculate F(n), and store the intermediate
results in the recursive function's additional arguments, which serve as
accumulators. The time to execute is, therefore n * time to execute
one addition and one recursive call. The addition of large
numbers if O(n), and recursive calls are typically constant time and never greater
than O(n). The time to execute the algorithm is T(n)=t0n2.
which is a straight line in the plot of sqrt(T) vs. n.
This recursive functions is easily written as tail recursion, which means
it does not contribute to space complexity, but space is needed to store
the accumulated sum, which grows as O(n). In the languages that do not support
tail recursion, such as C/C++, space grows as O(n2), and the
algorithm quickly becomes useless. Such languages are more suited for 2C (iteration) anyway.
|
| Language | Translator [*] | t0 | T(1,000,000),
seconds | |
|---|
| Haskell |
GHC 6.8.2 [c] |
12.4 fs |
12.42 |
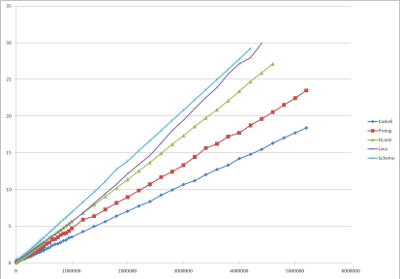
sqrt(Execution time, seconds) vs. Fibonacci number calculated
|
| Prolog |
SWI Prolog 5.7.15 [b] with GMP 4.3.1 |
21.3 fs |
22.22 |
| OCaml |
INRIA OCaml 3.11.1 [c] |
32.2 fs |
32.14 |
| Java |
Sun Java SE 1.6.0_16-b01 / HotSpot 64-Bit VM 14.2-b01 [b] |
34.1 fs |
31.27 |
| Scheme |
MIT Scheme 7.7.90 20090107 [b] |
48.8 fs |
47.88 |
| Forth |
GNU gforth 0.7.0 [i] |
- |
- |
| C++ |
GNU g++ 4.4.1 [c] with GMP 4.3.1 |
- |
- |
| J |
Jsoftware J64 6.02 [i] |
- |
- |
| |
|
|
|
[*] - [c] for Compiler, [b] for Bytecode intepreter, [i] for Interpreter
Execution time is user time as reported by time(1), the test programs were
modified to avoid conversion of the entire result to string, since that
operation may be slow for large numbers.
J reports stack overflow when trying to calculate numbers over ~3000,
and I could not find a way to increase available stack size in jconsole
C++ linked with GMP consumes memory at a very large pace, exceeding 20Gb when calculating
500,000th number
Forth (Gforth linked with GMP) also consumes memory at a very large pace, running into tens
of gigabytes about the 500,000th number
| ALGORITHM 2C: IMPERATIVE LOOP WITH MUTABLE VARIABLES |
|---|
- Assign value 0 to variable n1 and value 1 to variable n2
- Assign the value of n1+n2 to variable n2 and assign the old value of n2 to n1
- Repeat step 2 n times.
- Return the value of variable n1
Complexity (fixed precision): O(n) speed, O(1) space
Complexity (unlimited precision): O(n2) speed, O(n) space
These algorithms execute n additions to calculate F(n), and store the intermediate
results in mutable variables. Time to execute is, therefore n * time to execute
one addition and two variable read/store operations. The addition of large
numbers if O(n), and store/retrieve is typically constant time and never greater
than O(n). The time to execute the algorithm is T(n)=t0n2.
which is a straight line in the plot of sqrt(T) vs. n.
|
| Language | Translator [*] | t0 | T(1,000,000),
seconds | |
|---|
| Forth |
GNU gforth 0.7.0 [i] with GMP 4.3.1 |
11.1 fs |
11.13 |
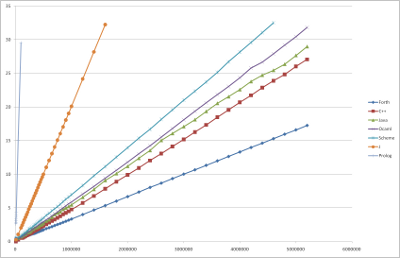
sqrt(Execution time, seconds) vs. Fibonacci number calculated
|
| C++ |
GNU g++ 4.4.1 [c] with GMP 4.3.1 |
23.2 fs |
22.62 |
| Java |
Sun Java SE 1.6.0_16-b01 / HotSpot 64-Bit VM 14.2-b01 [b] |
31.6 fs |
29.52 |
| OCaml |
INRIA OCaml 3.11.1 [c] |
35.9 fs |
34.52 |
| Scheme |
MIT Scheme 7.7.90 20090107 [b] |
50.8 fs |
48.46 |
| J |
Jsoftware J64 6.02 [i] |
413 fs |
403.6 |
| Prolog |
SWI Prolog 5.7.15 [b] with GMP 4.3.1 |
73.8 ns |
- |
| Haskell |
GHC 6.8.2 [c] |
- |
- |
| Hope |
Hope by Ross Paterson, 08-Dec-03 [i] |
- |
- |
| |
|
|
|
[*] - [c] for Compiler, [b] for Bytecode intepreter, [i] for Interpreter
Execution time is user time as reported by time(1), the test programs were
modified to avoid conversion of the entire result to string, since that
operation may be slow for large numbers.
Prolog usually does not have mutable variables, but some implementations do.
Haskell does not have the concept of mutable variables.
Hope does not have the concept of mutable variables.
| ALGORITHM 3A: MATRIX MULTIPLICATION |
|---|
This is the most mathematically elegant way to calculate a Fibonacci number.
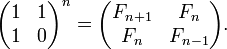
Complexity (fixed precision): O(log n) speed, O(1) space
Complexity (unlimited precision): O(n log2 n log log n) speed, O(n) space
Raising a matrix to the power of n requires only O(log n) matrix
multiplications, if n is a natural number and the repeated squaring algorithm
is used. Space requirements for repeated squaring include the product
accumulator and the last calculated square, which makes it O(1) (in fixed-precision case)
unless non-tail-recursive implementation is used.
In case of unlimited precision, execution time of each 2x2 matrix multiplication
is proportionate to the execution time of one integer multiplication,
which has the complexity of O(n log n log log n) and space requirements to store
one 2x2 matrix grow as O(n).
The repeated squaring algorithm for calculation of xn:
- start with product accumulator a=1 and last square accumulator s=x
- if n is odd, increase the accumulated product, a=a*s
- calculate the next square of s, s=s2
- divide n by 2, n = n div 2
- repeat until n=0, at which time the final value of a is the answer
In languages providing bit operations, this algorithm can examine the bits
in the binary representation of n, proceeding from least-significant
to most-significat bit, instead of repeating division by 2. The example in J
makes good use of this approach.
|
| Language | Translator [*] | t0 | T(1,000,000),
seconds | |
|---|
| |
|
|
|

sqrt(Execution time, seconds) vs. Fibonacci number calculated
|
| |
|
|
|
[*] - [c] for Compiler, [b] for Bytecode intepreter, [i] for Interpreter
Execution time is user time as reported by time(1), the test programs were
modified to avoid conversion of the entire result to string, since that
operation may be slow for large numbers.
| ALGORITHM 3B: FAST RECURSION |
|---|
This algorithm can be derived either from from the fact that, from definition,
F(n+m)=F(n)F(m) + F(n-1)F(m-1), or by rewriting the matrix equation using the
fact that An+m=AnAm:
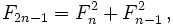
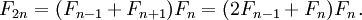
This algorithm is faster than than 3A because it does not repeat calculations
of the same numbers (top right and bottom left corners of the matrix in 3A),
but it cannot be easily implemented as a tail-recursive function, resulting
in O(log n) space complexity.
I implement it this way:
- Define a recursive function λ(n) such as
- λ(n) returns a pair of numbers (0,0) if n equals 0
- λ(n) returns a pair of numbers (1,0) if n equals 1
- recursively calculate λ(n div 2) (integer division,
(n-1)/2 for odd n) to obtain a pair of numbers (k2,k1)
- for even n, return a pair of numbers
(2k1+k2)*k2,
k12+k22)
- for odd n, return a pair of numbers
((k1+k2)2 ,
(2k1+k2)*k2)
- The end result is the first element of the result of λ(n)
Complexity (fixed precision): O(log n) speed, O(log n) space
Complexity (unlimited precision): O(n log2 n log log n) speed, O(n log n) space
|
| Language | Translator [*] | t0 | T(1,000,000),
seconds | |
|---|
| |
|
|
|

sqrt(Execution time, seconds) vs. Fibonacci number calculated
|
| |
|
|
|
[*] - [c] for Compiler, [b] for Bytecode intepreter, [i] for Interpreter
Execution time is user time as reported by time(1), the test programs were
modified to avoid conversion of the entire result to string, since that
operation may be slow for large numbers.
| ALGORITHM 3C: BINET'S FORMULA WITH ROUNDING |
|---|
Eigendecomposition of the matrix equation from 1A gives a formula,
published by Abraham de Moivre in 1730, Euler in 1765, and by Jacques Philippe
Marie Binet in 1843
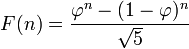
Where φ is the golden ratio, (1+sqrt(5))/2.
Because (1-phin) / sqrt(5) is less than 1/2 for all positive n, this
formula can be simplified to nearest integer to φn/sqrt(5) or,
using the floor function,
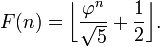
Complexity (fixed precision): O(log n) speed, O(1) space
Complexity (unlimited precision): O(n log2 n log log n) speed, O(n) space
Evaluation of this formula, just as evaluation of the formula in 3A, is thus
reduced to taking an integer power of a number, only this number is irrational
and must be represented as a floating-point value with sufficient precision to
produce the correct fibonacci number. Not many languages support arbitrary
precision floating point values, I use GNU MP library where possible.
The computational and space complexity of this algorithm are the same as 1A,
and are the same as the complexity of the repeated squaring algorithm with one
addition: time to calculate the square root of five with sufficient precision.
Where not provided by the compiler/library, I iteratively calculate inverse
square root via y(n+1) = 0.5*y(n)*[3 - a*y(n)^2] because this recurrent
expression has no division.
|
| Language | Translator [*] | t0 | T(1,000,000),
seconds | |
|---|
| |
|
|
|

sqrt(Execution time, seconds) vs. Fibonacci number calculated
|
| |
|
|
|
[*] - [c] for Compiler, [b] for Bytecode intepreter, [i] for Interpreter
Execution time is user time as reported by time(1), the test programs were
modified to avoid conversion of the entire result to string, since that
operation may be slow for large numbers.
LINKS
Wolfram's MathWorld entry
OEIS entry
|





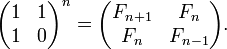

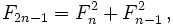
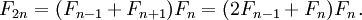
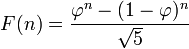
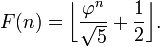
![[Valid CSS!]](http://cubbi.org/images/vcss.gif)
![[Valid ISO-HTML!]](http://cubbi.org/images/v15445.gif)
![[Powered by Linux]](http://cubbi.org/images/powered_by_linux.gif)